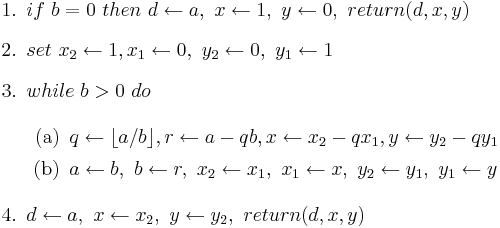Erweiterter Euklidischer Algorithmus
Zur Berechnung des grössten gemeinsamen Teilers zweier Zahlen (ggT) wird der euklidische Algorithmus benutzt. Der Erweiterte euklidische Algorithmus berechnet zusätzlich zum ggT noch zwei Faktoren x und y die folgende Bedingung erfüllen:
![]()
In der Kryptographie findet der Algorithmus vor allem Verwendung für die Berechnung von inversen Elementen in Restklassenkörpern. Beim RSA Verfahren wird der erweiterte euklidische Algorithmus zum Beispiel verwendet um ein Schlüsselpaar zu erstellen, bestehend aus einem geheimen und einem öffentlichen Schlüssel.
Als Input erwartet das Applet zwei ganzzahlige Integer a und b. Ziel ist es, den ggT(a,b) zu berechnen, sowie die zwei Faktoren des erweiterten Euklids.
Mit einem Klick auf Start werden die Variablen initialisiert. Die zwei Buttons erlauben anschliessend entweder eine schrittweise Berechnung oder ohne Zwischenhalte.
Die Farben rot und blau zeigen die wichtigste Zuordnung bei jedem Schritt. Nach Ausführung zeigen die grünen Felder, wo die Lösung abgelesen werden kann.
Folgender Pseudocode zeigt die Funktionsweise des verwendeten Algorithmus auf: